- Numbers
- What does the number stand for?
- Nearest number
- Which digit is in the place?
- Round off to the nearest number
- Number divide
- Find the fraction nearest to 1
- Sort fraction numbers
- Find the largest or smallest fraction
- Fraction to decimal
- Convert decimal to a mixed fraction.
- Fraction - Addition
- Fraction - Substraction
- Fraction - Multiply
- Fraction - Divide
- List all the common factors of two integers
- Chicken and Rabbit problem
- Assumption Method
- Measurement
- Data Analysis
- Geometry
- Speed
- Others
- P5 Maths
- P4 Maths
- Tap to switch levels
- Numbers
- Measurement
- Data Analysis
- Geometry
- Speed
- Others
- P5 Maths
- P4 Maths
SELECT A SUBJECT
- Numbers
Question 1 of 79
The figure below shows two identical semicircles with radius 8cm each. Find the perimeter of the shaded part.
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of a big semicircle and two identical small semicircles. What is the perimeter of the figure if the radius of the big semicircle is 14cm? $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
Regions A, B and C represent the number of point assigned to the three target as shown below. The total points in Region A and B, B and C, and A and C are 11. 19 and 16 respectively. How many points is assigned to region A?
Sorry. Please check the correct answer below.
4 Points $\rightarrow$ $11 + 19 + 16 = 46$
$46 ÷ 2 = 23$
$23 – 19 = 4$
You are Right
4 Points $\rightarrow$ $11 + 19 + 16 = 46$
$46 ÷ 2 = 23$
$23 – 19 = 4$
The figure shown three semicircles and a circle. AB = BC = CD = DE = 5cm, find the perimeter of the shaded part. Give your answer in 2 decimal places.
Sorry. Please check the correct answer below.
Circumference of Semi: $10 \times 3.142 \times \frac{1}{2} = 15.71$
Circumference of quarter: $15.71 ÷ 2 = 7.855$
Circumference of big quarter: $20 \times 3.142 \times \frac{1}{4} = 15.71$
$15.71 + 7.855 + 7.855 + 15.71 = 47.13cm$
You are Right
Circumference of Semi: $10 \times 3.142 \times \frac{1}{2} = 15.71$
Circumference of quarter: $15.71 ÷ 2 = 7.855$
Circumference of big quarter: $20 \times 3.142 \times \frac{1}{4} = 15.71$
$15.71 + 7.855 + 7.855 + 15.71 = 47.13cm$
The figure below is made up a quadrant and a semi-circle. Find the perimeter of the shaded figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
$\frac{1}{4} \times 28 \times \frac{22}{7} = 22$
$\frac{1}{2} \times 14 \times \frac{22}{7} = 22$
$14 + 22 + 22 = 58cm$
You are Right
$\frac{1}{4} \times 28 \times \frac{22}{7} = 22$
$\frac{1}{2} \times 14 \times \frac{22}{7} = 22$
$14 + 22 + 22 = 58cm$
The figure below shows a circle with center O. Given that AC = AB and $\angle$OBC = 40$^\circ$, Find $\angle$CAB.
Sorry. Please check the correct answer below.
You are Right
Find the area of the quarter circle below. Take $\pi$ = 3.14.
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of a semi- circle, 2 small quadrants and a rectangle. O is the center of the semi- circle. The diameter of the semi – circle is 32cm and the radius of each quadrant is 8cm. Find the area of the shaded parts. $(Take\pi = 3.14)$
Sorry. Please check the correct answer below.
Area of Semi-Circle = $\frac{1}{2} \times \pi \times 16 \times 16 = 128\pi$cm$^2$
Area of 2 quadrant = $\frac{1}{2} \times \pi \times 8 \times 8 = 32\pi$cm$^2$
Area of crescents = $8 \times 8 \times 2 – 32\pi = 128 – 32\pi$cm$^2$
Area of rectangle = $16 \times 8 = 128cm^2$
Area of shaded parts = $128\pi – 128 – (128 – 32\pi) = 160\pi – 256 = 246.4cm^2$
You are Right
Area of Semi-Circle = $\frac{1}{2} \times \pi \times 16 \times 16 = 128\pi$cm$^2$
Area of 2 quadrant = $\frac{1}{2} \times \pi \times 8 \times 8 = 32\pi$cm$^2$
Area of crescents = $8 \times 8 \times 2 – 32\pi = 128 – 32\pi$cm$^2$
Area of rectangle = $16 \times 8 = 128cm^2$
Area of shaded parts = $128\pi – 128 – (128 – 32\pi) = 160\pi – 256 = 246.4cm^2$
The figure below is formed by of 4 identical quarter circles, 1 semicircle and 1 rectangle. Find the area of the shaded figure. Leave your answer in terms of $\pi$.
Sorry. Please check the correct answer below.
You are Right
In the figure shown below, O is the center of the circle. OS = ST and ROT is a straight line. Find (a) $\angle$ TOS
(b) $\angle$ TRS
30$^\circ$
40$^\circ$
50$^\circ$
60$^\circ$
Sorry. Please check the correct answer below.
(a) 60$^\circ$ $\rightarrow$ $\angle$ $TOS = 180^\circ ÷ 3 = 60^\circ$
(b) 30$^\circ$ $\rightarrow$ $\angle$ $TRS = 180^\circ – 120^\circ ÷ 2 = 30^\circ$
30$^\circ$
You are Right
(a) 60$^\circ$ $\rightarrow$ $\angle$ $TOS = 180^\circ ÷ 3 = 60^\circ$
(b) 30$^\circ$ $\rightarrow$ $\angle$ $TRS = 180^\circ – 120^\circ ÷ 2 = 30^\circ$
The figure below is formed by large semicircle, 2 small identical semicircles and a straight line. The semicircles are formed along the edges of a right- angled triangle. The dimension of the triangle are 3cm, 4cm and 5cm.
(a) Find the perimeter of the figure.
(b) Find the area of the figure, correct to 2 decimal places. Take $\pi$ = 3.14
(b) 13.81cm$^2$
(b) 14.81cm$^2$
(b) 15.81cm$^2$
(b) 16.81cm$^2$
Sorry. Please check the correct answer below.
(a)Diameter of small semi $\rightarrow$ 2
Perimeter of 2 small semi $\rightarrow$ $\pi \times d$
= $3.14 \times 2$
6.28
Perimeter of 1 big semi $\rightarrow$ $\pi \times d \times \frac{1}{2}$
$3.14 \times 5 \times \frac{1}{2} = 7.85$
Perimeter of figure $\rightarrow$ $7.85 + 6.28 + 3 = 17.13cm$ (b) $\bigtriangleup$ $\rightarrow$ $\frac{1}{2} \times 3 \times 4 = 6$
$5 \div 2 = 2.5$
Semi $\rightarrow$ $\pi \times r \times r \times \frac{1}{2}$
= $3.14 \times 2.5 \times 2.5 \times \frac{1}{2} = 9.81$
Total area $\rightarrow$ $6 + 9.81 = 15.81cm^2$
(b) 15.81cm$^2$
You are Right
(a)Diameter of small semi $\rightarrow$ 2
Perimeter of 2 small semi $\rightarrow$ $\pi \times d$
= $3.14 \times 2$
6.28
Perimeter of 1 big semi $\rightarrow$ $\pi \times d \times \frac{1}{2}$
$3.14 \times 5 \times \frac{1}{2} = 7.85$
Perimeter of figure $\rightarrow$ $7.85 + 6.28 + 3 = 17.13cm$ (b) $\bigtriangleup$ $\rightarrow$ $\frac{1}{2} \times 3 \times 4 = 6$
$5 \div 2 = 2.5$
Semi $\rightarrow$ $\pi \times r \times r \times \frac{1}{2}$
= $3.14 \times 2.5 \times 2.5 \times \frac{1}{2} = 9.81$
Total area $\rightarrow$ $6 + 9.81 = 15.81cm^2$
The figure below is made up 1 circle, 3 identical rectangles and 12 identical quarter circle of radius 10cm
(a) Find the perimeter of the unshaded part, X
(b)Find the total area of the shaded parts. $(Take \pi = 3.14)$.
(b) 1512cm$^2$
(b) 1514cm$^2$
(b) 1515cm$^2$
(b) 1516cm$^2$
Sorry. Please check the correct answer below.
(a)82.8 $\rightarrow$ $3.14 \times 20 = 62.8$
$62.8 ÷ 2 = 31.4$
Perimeter = $31.4 + 31.4 + 10 + 10 = 82.8$
(b)1514cm$^2$ $\rightarrow$ Area = $12 \times 10 \times 10 + 3.14 \times 10 \times 10 = 1514$cm$^2$
(b) 1514cm$^2$
You are Right
(a)82.8 $\rightarrow$ $3.14 \times 20 = 62.8$
$62.8 ÷ 2 = 31.4$
Perimeter = $31.4 + 31.4 + 10 + 10 = 82.8$
(b)1514cm$^2$ $\rightarrow$ Area = $12 \times 10 \times 10 + 3.14 \times 10 \times 10 = 1514$cm$^2$
The figure consists of a big semicircle of radius 10cm and 4 small quadrants each of radius 5cm. Find the perimeter of the shaded part. Leave your answer in terms of $\pi$.
Sorry. Please check the correct answer below.
$\pi \times 10 = 10\pi$
$\frac{1}{2} \times \pi \times 20 = 10\pi$
$10\pi + 10\pi = 20\pi$
You are Right
$\pi \times 10 = 10\pi$
$\frac{1}{2} \times \pi \times 20 = 10\pi$
$10\pi + 10\pi = 20\pi$
The figure is made up of a semicircle and an equilateral triangle. The diameter of the semicircle is 10cm. What is the perimeter of the figure?
Sorry. Please check the correct answer below.
Semi Circle $\rightarrow$ $\frac{1}{2} \times \pi \times 15 = 5\pi$cm
Triangle $\rightarrow$ $10 \times 2 = 20cm$
Total $\rightarrow$ $5\pi$cm + $20cm = (5\pi +20)$cm
You are Right
Semi Circle $\rightarrow$ $\frac{1}{2} \times \pi \times 15 = 5\pi$cm
Triangle $\rightarrow$ $10 \times 2 = 20cm$
Total $\rightarrow$ $5\pi$cm + $20cm = (5\pi +20)$cm
The figure below is made up of two identical quarter circles of radius 3cm. What is the perimeter of the figure?
Sorry. Please check the correct answer below.
You are Right
The figure below shows 3 identical overlapping circles. The middle circle touches the center of the other 2 circles. Line AB is the diameter of the middle circle. What fraction is unshaded?
Sorry. Please check the correct answer below.
$\frac{4}{16$} = $\frac{1}{4}$
You are Right
$\frac{4}{16$} = $\frac{1}{4}$
The figure below is made up of a semicircle and a right-angled isosceles triangle ABC. AB= BC and the diameter of the semicircle is 28cm. Find the area of the shaded part of the figure.
Sorry. Please check the correct answer below.
$\frac{1}{2} \times 28 \times 14 = 196$cm$^2$
You are Right
$\frac{1}{2} \times 28 \times 14 = 196$cm$^2$
The figure shows a quarter circle in a semicircle. The diameter of the semicircle is 14cm. Find the area of the unshaded parts. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The figure shows two quadrants of circles, centered at C and D respectively. Find the difference between the area of the two shaded regions. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
Area of rectangle $\rightarrow$ $(28\times14) cm^2 = 392cm^2$
Area of quadrent $\rightarrow$ $(28\times 28 \times \frac{22}{7})cm^2 ÷ 4 = 616cm^2$
Area of A,B and small quadrent $\rightarrow$ $(616 - 392)cm^2 ÷ 4 = 224cm^2$
Area of A and B $\rightarrow$ $(224 -154)cm^2 = 70cm^2$
Area of H and B $\rightarrow$ $(616 - 154)cm^2 = 462cm^2$
Difference in two shaded parts $\rightarrow$ $(462-392)cm^2 = 70cm^2$
You are Right
Area of rectangle $\rightarrow$ $(28\times14) cm^2 = 392cm^2$
Area of quadrent $\rightarrow$ $(28\times 28 \times \frac{22}{7})cm^2 ÷ 4 = 616cm^2$
Area of A,B and small quadrent $\rightarrow$ $(616 - 392)cm^2 ÷ 4 = 224cm^2$
Area of A and B $\rightarrow$ $(224 -154)cm^2 = 70cm^2$
Area of H and B $\rightarrow$ $(616 - 154)cm^2 = 462cm^2$
Difference in two shaded parts $\rightarrow$ $(462-392)cm^2 = 70cm^2$
The figure shows two identical semicircles. O and P are the centers of the semicircles. $\frac{1}{5}$ of each semicircle is shaded. Find the total area of the shaded parts. $ (Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
1. D $\rightarrow$ $6 \div 2 = 30$
r $\rightarrow$ $30 \div 2 = 15$
$3.14 \times 15 \times 15 = 706.5$
Total $\rightarrow$ 10u
Shaded $\rightarrow$ 2u
$706.5 \div 10 = 70.65$
$70.65 \times 2 = 141.3$
You are Right
1. D $\rightarrow$ $6 \div 2 = 30$
r $\rightarrow$ $30 \div 2 = 15$
$3.14 \times 15 \times 15 = 706.5$
Total $\rightarrow$ 10u
Shaded $\rightarrow$ 2u
$706.5 \div 10 = 70.65$
$70.65 \times 2 = 141.3$
The diagram below is made up of a quarter and three- quarter circle with center O. Find the perimeter of the figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
A boomerang as shown in the figure below is made up of 3 identical small quadrants and 1 big quadrant. The radius of each small quadrant is 2cm and the radius of the big quadrant is 6cm. For each of the following, use the calculator value of $\pi$ to find.
(a) The perimeter of the shaded figure.
(b) The area of the shaded figure.
(b) 3.8cm$^2$
(b) 4.8cm$^2$
(b) 5.8cm$^2$
(b) 6.8cm$^2$
Sorry. Please check the correct answer below.
$\frac{1}{4} \times \pi \times 12 = 3\pi$
$\frac{1}{4} \times pi \times 4 = 1\pi$
$3\pi \pi + \pi + \pi = 6\pi$
Perimeter = $6\pi$ = 18.8cm
(b) $\frac{1}{4} \times \pi \times 6 \times 6 = 9\pi$
$\frac{1}{4} \times \pi \times 2 \times 2 = 1\pi$
$2 \times 2 = 4$
$4 \times 3 = 12$
Area = $9\pi – 3\pi -12 = 6.8cm^2$
(b) 6.8cm$^2$
You are Right
$\frac{1}{4} \times \pi \times 12 = 3\pi$
$\frac{1}{4} \times pi \times 4 = 1\pi$
$3\pi \pi + \pi + \pi = 6\pi$
Perimeter = $6\pi$ = 18.8cm
(b) $\frac{1}{4} \times \pi \times 6 \times 6 = 9\pi$
$\frac{1}{4} \times \pi \times 2 \times 2 = 1\pi$
$2 \times 2 = 4$
$4 \times 3 = 12$
Area = $9\pi – 3\pi -12 = 6.8cm^2$
Find the perimeter of a $\frac{3}{4}$ circle of radius 28cm. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
In the figure below which is not dram to scale, EFGH is a parallelogram. O is the center of the circle. Find
(a) $\angle$x
(b) $\angle$y
(b) 100$^\circ$
(b) 120$^\circ$
(b) 140$^\circ$
(b) 180$^\circ$
Sorry. Please check the correct answer below.
(a) 90$^\circ$
(b) $\angle$HFO = $\angle$OEF = $\angle$ OFE = 60$^\circ$
$\angle$HFO = Isosceles
$\angle$ FHO = $\angle$HFO = $(180^\circ - 120^\circ) ÷ 2 = 30^\circ$
$\angle$x = $30^\circ + 60^\circ = 90^\circ$
$\angle$ GFE = $\angle$GHO = $\angle$y = 120$^\circ$
(b) 120$^\circ$
You are Right
(a) 90$^\circ$
(b) $\angle$HFO = $\angle$OEF = $\angle$ OFE = 60$^\circ$
$\angle$HFO = Isosceles
$\angle$ FHO = $\angle$HFO = $(180^\circ - 120^\circ) ÷ 2 = 30^\circ$
$\angle$x = $30^\circ + 60^\circ = 90^\circ$
$\angle$ GFE = $\angle$GHO = $\angle$y = 120$^\circ$
The figure below is not scale. Line AB is 36cm and it cuts through the center of all four circles. Find the perimeter of the figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of an isosceles triangle and a circle with center O. The area of the isosceles triangle is 81cm$^2$. $(Take\pi = 3.14)$, Find the circumference of the circle.
Sorry. Please check the correct answer below.
$\frac{1}{2} \times 9 \times 18 = 81$
You are Right
$\frac{1}{2} \times 9 \times 18 = 81$
The figure below is made up of 3 semi-circles. Find the area of the figure. $(Take \pi= \frac{22}{7})$
Sorry. Please check the correct answer below.
464cm$^2$ $\rightarrow$ $14 ÷ 2 =7$
$\frac{22}{7} \times 7 \times 7 = 154$
$\frac{22}{7} \times 14 \times 14 ÷ 2 = 44 \times 14 ÷ 2 = 616 ÷ 2 = 308$
$308 + 154 = 462$
You are Right
464cm$^2$ $\rightarrow$ $14 ÷ 2 =7$
$\frac{22}{7} \times 7 \times 7 = 154$
$\frac{22}{7} \times 14 \times 14 ÷ 2 = 44 \times 14 ÷ 2 = 616 ÷ 2 = 308$
$308 + 154 = 462$
A path is constructed around a circular garden. The path has a width of 3m. Find the area of the path. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
$\frac{22}{7} \times 7 \times 7 \times 7 = 154$
$\frac{22}{7} \times 10 \times 10 = 314_\frac{2}{7}$
$314_\frac{2}{7} – 154 = 160_\frac{2}{7}m_2$
You are Right
$\frac{22}{7} \times 7 \times 7 \times 7 = 154$
$\frac{22}{7} \times 10 \times 10 = 314_\frac{2}{7}$
$314_\frac{2}{7} – 154 = 160_\frac{2}{7}m_2$
The figure is made up of 3 identical quarter circle and a right- angled isosceles triangle. $\angle$ABC = 90$^\circ$ and AB = BC The length of AC is 6cm. Find the area of the figure. Take $\pi$ = 3.14
Sorry. Please check the correct answer below.
Area of square $\rightarrow$ $6 \times 6 = 36$
Atra of 1 triangle $\rightarrow$ $36 \div 4 = 9$
Area of 2 triangle $\rightarrow$ $9 \times 2 = 18$
Area of $\frac{3}{4}$ circle $\rightarrow$ $\frac{3}{4} \times \pi \times r \times r$
$\rightarrow$ $\frac{3}{4} \times \pi \times \sqrt(18) \times \sqrt(18)$
$\rightarrow$ $\frac{3}{4} \times 3.14 \times \sqrt(18) \times \sqrt(18)$
$\rightarrow$ 42.39
Area of figure $\rightarrow$ $42.39 + 9 = 51.39cm^2$
You are Right
Area of square $\rightarrow$ $6 \times 6 = 36$
Atra of 1 triangle $\rightarrow$ $36 \div 4 = 9$
Area of 2 triangle $\rightarrow$ $9 \times 2 = 18$
Area of $\frac{3}{4}$ circle $\rightarrow$ $\frac{3}{4} \times \pi \times r \times r$
$\rightarrow$ $\frac{3}{4} \times \pi \times \sqrt(18) \times \sqrt(18)$
$\rightarrow$ $\frac{3}{4} \times 3.14 \times \sqrt(18) \times \sqrt(18)$
$\rightarrow$ 42.39
Area of figure $\rightarrow$ $42.39 + 9 = 51.39cm^2$
The figure below is made up of two semicircles. O is the center of the larger semicircle of radius 8cm. Find the perimeter of the figure.
Sorry. Please check the correct answer below.
You are Right
A circular hoopla hoop of radius 10cm is cut into 4 equal pieces and re-arranged to make the shape as shown. What is the perimeter of the shape? $ (Take\pi = 3.14)$
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of a quadrant and 2 identical semicircles. AC is twice of AD. What is the perimeter of the shaded figure below? $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
O is the center of the large circle and AO is the diameter of the small circle. The diameter of the large circle is 2 times the diameter of the small circle. The circumferences of the big and small circle meet each other at point A. The perimeter of the shaded figure is 30$\pi$ cm, what is the diameter of the small circle?
Sorry. Please check the correct answer below.
Perimeter of small circle = $\pi$d
Perimeter of big circle = $\pi$ + 2d = 2$\pi$d
Total perimeter of figure = $\pi$ d + 2 $\pi$ d
= 3d – 30$\pi$
d = 10cm
You are Right
Perimeter of small circle = $\pi$d
Perimeter of big circle = $\pi$ + 2d = 2$\pi$d
Total perimeter of figure = $\pi$ d + 2 $\pi$ d
= 3d – 30$\pi$
d = 10cm
In the figure below, a square lies within a circle. Given that the square has an area of 98cm$^2$, Find the total area of the shaded parts. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The figure below is formed by overlapping a square and a circle. O is the center of the circle. The radicle is 14cm. Find the perimeter of the figure. $(Take \pi= \frac{22}{7})$
Sorry. Please check the correct answer below.
You are Right
The figure below comprises 5 circle. Circle A is identical to circle B. Circle C is identical to circle D. The ratio of the area of circle A to the area of circle C to the area of circle E is 1 : 4 : 16. If the diameter of circle C is 8cm, find the total perimeter of shaded regions.
Sorry. Please check the correct answer below.
$8 ÷ 2 = 4$
$pi \times 4 \times 4 = 16\pi$
$16\pi \div 4 = 4\pi$
$4\pi \div \pi = 4$
$2 \times 2 = 4$
$2 + 2 = 4$
$4 \times \pi = 4\pi$
$4\pi \times 2 = 8\pi$
$8\pi \times 2 = 16\pi$
$8\pi + 16\pi = 24\pi$cm
You are Right
$8 ÷ 2 = 4$
$pi \times 4 \times 4 = 16\pi$
$16\pi \div 4 = 4\pi$
$4\pi \div \pi = 4$
$2 \times 2 = 4$
$2 + 2 = 4$
$4 \times \pi = 4\pi$
$4\pi \times 2 = 8\pi$
$8\pi \times 2 = 16\pi$
$8\pi + 16\pi = 24\pi$cm
The figure below is made up of semicircles. Find the perimeter of the figure below. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
In the figure below, not drawn to scale, O is the center of the semi-c ircle. PR = RS, QT //RS and $\angle$PRS = 86$^\circ$. Find $\angle$OPT.
Sorry. Please check the correct answer below.
$180^\circ - 86^\circ = 94^\circ $
$180^\circ - 94^\circ = 86^\circ $
$(180^\circ - 86^\circ) ÷ 2 = 46^\circ$
$47^\circ + 86^\circ = 133^\circ$
$\angle$OPT = $(180^\circ - 133^\circ) ÷ 2 = 23.5^\circ$
You are Right
$180^\circ - 86^\circ = 94^\circ $
$180^\circ - 94^\circ = 86^\circ $
$(180^\circ - 86^\circ) ÷ 2 = 46^\circ$
$47^\circ + 86^\circ = 133^\circ$
$\angle$OPT = $(180^\circ - 133^\circ) ÷ 2 = 23.5^\circ$
How many more circles must be shaded so that the fraction of the number of unshaded circles is$\frac{1}{4}$ of the total number of circles?
Sorry. Please check the correct answer below.
You are Right
The figure shown is made up of three identical small circles and a Larger circle with radius 10cm.Find the ratio of the unshaded area to the shaded area. $ (Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of one big semi-circle is 4 identical small semi-circles. The diameter of each small semi-circle is 14cm. Find the perimeter of the shaded area of the figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
$2 \times \frac{22}{7} \times 14 = 88$
$\frac{1}{2} \times \frac{22}{7} \times56 = 88$
$88 \times 2 = 176cm$
You are Right
$2 \times \frac{22}{7} \times 14 = 88$
$\frac{1}{2} \times \frac{22}{7} \times56 = 88$
$88 \times 2 = 176cm$
Three circle are placed side- by- side as show. PQ is 7.5cm and it cuts through the centers of all circle. Find the circumference of the 3 circle Take$\pi$ = 3.14
Sorry. Please check the correct answer below.
$3.14 \times 7.5 = 23.55cm$
You are Right
$3.14 \times 7.5 = 23.55cm$
The figure below is made up of 3 different semi-circle. The radius of the smallest semi-circle is 3cm. Using $\pi$ = 3.14, Find the area of the shaded part.
Sorry. Please check the correct answer below.
Big $\rightarrow$ $\frac{1}{2} \times \pi \times 5 \times 5 = 12\frac{1}{2}\pi$
Medium $\rightarrow$ $\frac{1}{2} \times \pi \times 4 \times 4 = 8\pi$
Small $\rightarrow$ $\frac{1}{2} \times \pi \times 3 \times 3 = 4.5\pi$
$\rightarrow$ $(12.5\pi – 4.5\pi) + 8\pi = 16\pi$
You are Right
Big $\rightarrow$ $\frac{1}{2} \times \pi \times 5 \times 5 = 12\frac{1}{2}\pi$
Medium $\rightarrow$ $\frac{1}{2} \times \pi \times 4 \times 4 = 8\pi$
Small $\rightarrow$ $\frac{1}{2} \times \pi \times 3 \times 3 = 4.5\pi$
$\rightarrow$ $(12.5\pi – 4.5\pi) + 8\pi = 16\pi$
The figure below shows a small circle of diameter 12cm inside a big circle of radius 12cm. Find the area of the unshaded part of the big circle.
Sorry. Please check the correct answer below.
$\pi \times 12 \times 12 = 144\pi$
$\pi \times 6 \times 6 = 36\pi$
$144\pi – 36\pi = 108\pi$
You are Right
$\pi \times 12 \times 12 = 144\pi$
$\pi \times 6 \times 6 = 36\pi$
$144\pi – 36\pi = 108\pi$
In the figure, OR, OP, PQ and QR are straight line. The points O, P, Q and R are the centers of the four circle. The radius of each is 15cm. Find the total perimeter of the shaded parts.
Sorry. Please check the correct answer below.
Perimeter = 2$\pi$r + $8 \times 15 = 30\pi + 120cm$
You are Right
Perimeter = 2$\pi$r + $8 \times 15 = 30\pi + 120cm$
The figure is made up of four semi – circle and a rectangle ABCD. AB = 9cm, BC = 12cm and AC 15cm. Find the total area of the shaded parts. $ (Take \pi = 3.14)$.
Sorry. Please check the correct answer below.
$\frac{1}{2} \times 9 \times 12 = 54cm^2$
$\frac{1}{2} \times 3.14 \times 4.5 \times 4.5 = 31.79cm^2$
$\frac{1}{2} \times 3.14 \times 6 \times 6 = 56.52cm^2$
$54 + 31.79 + 56.52 = 142.31cm^2$
$\frac{1}{2} \times 3.14 \times 7.5 \times 7.5 = 88.31cm^2$
142.31 – 88.31 = 54cm^2$
$54 \times 2 = 108cm^2$
You are Right
$\frac{1}{2} \times 9 \times 12 = 54cm^2$
$\frac{1}{2} \times 3.14 \times 4.5 \times 4.5 = 31.79cm^2$
$\frac{1}{2} \times 3.14 \times 6 \times 6 = 56.52cm^2$
$54 + 31.79 + 56.52 = 142.31cm^2$
$\frac{1}{2} \times 3.14 \times 7.5 \times 7.5 = 88.31cm^2$
142.31 – 88.31 = 54cm^2$
$54 \times 2 = 108cm^2$
In the figure, the circle touches each of the two equilateral triangle at exactly three points. What fraction of the figure is shaded?
Sorry. Please check the correct answer below.
You are Right
The figure below is created with 4 quarter circles and a square.
(a) The unshaded part marked A is enclosed by the quarter and quarter circle. Find the area of A.
(b) Find the area of the shaded figure. $ (Take\pi = 3.14)$.
(b) 9.6 cm$^2$
(b) 9.12 cm$^2$
(b) 11.6 cm$^2$
(b) 11.12 cm$^2$
Sorry. Please check the correct answer below.
$6cm \times 6cm \times \frac{1}{4} \times 3.14 = 28.26cm^2$
$6cm \times 6cm = 36 cm^2$
(a) $36 cm^2 – 28.26 cm^2 = 7.74 cm^2$
$4cm \times 4cm \times 3.14 \times \frac{1}{4} = 12.56 cm^2$
$4cm \times 4cm = 16 cm^2$
$16 cm^2 – 12.56 cm^2 = 3.44cm^2$
$2cm \times 4cm = 8cm^2$
$36cm^2 – 3.44 cm^2 - 8 cm^2 = 24.56cm^2$
$24.56 cm^2 – 7.74 cm^2 = 16.82 cm^2$
$2cm \times 2cm = 4 cm^2$
$12.56 cm^2- 4 cm^2 = 8.56 cm^2$
$2cm \times 2cm \times 3.14 \times \frac{1}{4} = 3.14 cm^2$
$12.82 cm^2 – 3.14 cm^2 – 8.56 cm^2 = 5.12 cm^2$
(b) $5.12 cm^2 + 4 cm^2 = 9.12 cm^2$
(b) 9.12 cm$^2$
You are Right
$6cm \times 6cm \times \frac{1}{4} \times 3.14 = 28.26cm^2$
$6cm \times 6cm = 36 cm^2$
(a) $36 cm^2 – 28.26 cm^2 = 7.74 cm^2$
$4cm \times 4cm \times 3.14 \times \frac{1}{4} = 12.56 cm^2$
$4cm \times 4cm = 16 cm^2$
$16 cm^2 – 12.56 cm^2 = 3.44cm^2$
$2cm \times 4cm = 8cm^2$
$36cm^2 – 3.44 cm^2 - 8 cm^2 = 24.56cm^2$
$24.56 cm^2 – 7.74 cm^2 = 16.82 cm^2$
$2cm \times 2cm = 4 cm^2$
$12.56 cm^2- 4 cm^2 = 8.56 cm^2$
$2cm \times 2cm \times 3.14 \times \frac{1}{4} = 3.14 cm^2$
$12.82 cm^2 – 3.14 cm^2 – 8.56 cm^2 = 5.12 cm^2$
(b) $5.12 cm^2 + 4 cm^2 = 9.12 cm^2$
The figure below shows a quadrant and a semicircle enclosed with in a square. O is the center of the square. The square has a length of 12cm.
(a) Find the area of the shaded part.
(b) Find the perimeter of the shaded part $(Take\pi = 3.14)$
(b) 31.22cm
(b) 31.42cm
(b) 33.22cm
(b) 33.42cm
Sorry. Please check the correct answer below.
(a) 43.74cm$^2$ $\rightarrow$ $12 \times 12 = 144$
$144 ÷ 2 = 72$
$3.14 \times (12 ÷ 2) \times (12 ÷ 2)$ = 113.04
$113.04 ÷ 4 = 28.26$
$72 – 28.26 = 43.74$
(b) 33.42cm $\rightarrow$ $3.14 \times 12 = 37.68$
$37.68 ÷ 4 = 9.42$
$9.24 + 6 + 6 + 12 = 33.42$
(b) 33.42cm
You are Right
(a) 43.74cm$^2$ $\rightarrow$ $12 \times 12 = 144$
$144 ÷ 2 = 72$
$3.14 \times (12 ÷ 2) \times (12 ÷ 2)$ = 113.04
$113.04 ÷ 4 = 28.26$
$72 – 28.26 = 43.74$
(b) 33.42cm $\rightarrow$ $3.14 \times 12 = 37.68$
$37.68 ÷ 4 = 9.42$
$9.24 + 6 + 6 + 12 = 33.42$
The figure below is made up of 2 identical smaller semicircles and a bigger semicircle. O is the center of the bigger semicircle of radius 7cm. Find the perimeter of the whole figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
Janet cut out circles of the same size and pasted them on a rectangular strip of paper as shown below. AB and CD are diameters of the circles. What is the total area of the shaded parts? $ (Take \pi= 3.14)$
Sorry. Please check the correct answer below.
2322cm$^2$ $\rightarrow 120 ÷ 4 = 30$
$ 3.14 \times 30 \times 30 = 2826$
$30 \times 2 = 60$, $ 60 \times 60 = 3600$
$3600 – 2826 = 774$
$774 ÷ 4 = 1935$
No of Shaded $\rightarrow$ 12
$12 \times 193.5 = 2322$
You are Right
2322cm$^2$ $\rightarrow 120 ÷ 4 = 30$
$ 3.14 \times 30 \times 30 = 2826$
$30 \times 2 = 60$, $ 60 \times 60 = 3600$
$3600 – 2826 = 774$
$774 ÷ 4 = 1935$
No of Shaded $\rightarrow$ 12
$12 \times 193.5 = 2322$
The figure below is made up of 2 identical small circle and a big circle. The dotted line represents the diameter of the big circle. What fraction of the figure is shaded?
Sorry. Please check the correct answer below.
You are Right
The figure below shows a quarter circle of radius 10cm two identical quarter circle of radius 7cm. Find the perimeter of the figure in terms of $\pi$.
Sorry. Please check the correct answer below.
Diameter of B = $7 \times 2 = 14$
Diamterer of A = $10 \times 2 = 20$
Perimeter = $(\frac{1}{4} \times \pi \times 14) + (\frac{1}{4} \times \pi \times 14) + (\frac{1}{4} \times 20 \times \pi) + 7 + 7 + (10 - 7) + (10 - 7) = 3.5\pi + 3.5\pi + 5\pi + 20 = 12\pi = 20$
You are Right
Diameter of B = $7 \times 2 = 14$
Diamterer of A = $10 \times 2 = 20$
Perimeter = $(\frac{1}{4} \times \pi \times 14) + (\frac{1}{4} \times \pi \times 14) + (\frac{1}{4} \times 20 \times \pi) + 7 + 7 + (10 - 7) + (10 - 7) = 3.5\pi + 3.5\pi + 5\pi + 20 = 12\pi = 20$
The figure below shows a semicircle. Fine the perimeter of the semicircle.
Sorry. Please check the correct answer below.
You are Right
The figure below, not drawn to scale. Is a circle with O as the center. TS and RW are straight line. The ratio of $\angle$RSO to $\angle$OSW is 2 : 1. $\angle$SWO = 73$^\circ$. Find $\angle$TRS.
Sorry. Please check the correct answer below.
$(180^\circ - 90^\circ - 73^\circ) \times 2 = 34^\circ$
$45^\circ + (180^\circ - 34^\circ - 90^\circ) = 101^\circ$
You are Right
$(180^\circ - 90^\circ - 73^\circ) \times 2 = 34^\circ$
$45^\circ + (180^\circ - 34^\circ - 90^\circ) = 101^\circ$
The figure below is made up of a circle, a parallelogram and two identical semi-circle. The diameter of the circle, PR is 12cm and the diameter of the semi-circle is 6cm. PR is perpendicular to SP and RQ. Find the area of the shaded parts. $(Take \pi = 3.14)$
Sorry. Please check the correct answer below.
69.3cm$^2$ $\rightarrow$ $6cm \times 12cm = 72cm$
$113.04cm^2 - 72cm^2 = 41.04cm$
$\frac{1}{2} \times 3.14 \times 3cm \times 3cm = 14.13cm$
$1413 \times 2 = 28.26$cm
$41.04cm + 2826 = 69.3cm$
You are Right
69.3cm$^2$ $\rightarrow$ $6cm \times 12cm = 72cm$
$113.04cm^2 - 72cm^2 = 41.04cm$
$\frac{1}{2} \times 3.14 \times 3cm \times 3cm = 14.13cm$
$1413 \times 2 = 28.26$cm
$41.04cm + 2826 = 69.3cm$
The figure below is formed by a square and 2 semicircles of diameter diameter 6cm. Find the perimeter of the figure. Leave your answer in terms of $\pi$
Sorry. Please check the correct answer below.
You are Right
The figure is made of a quadrant and a semicircle. The quadrant has a radius of 21cm. what is the perimeter of the unshaded part? $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
A $\rightarrow$ $\frac{1}{2} \times 21 \times \frac{22}{7} = 33$
B $\rightarrow$ $\frac{1}{4} \times 21 \times \frac{22}{7} = 33$
P $\rightarrow$ $33 + 33 + 21 = 87cm$
You are Right
A $\rightarrow$ $\frac{1}{2} \times 21 \times \frac{22}{7} = 33$
B $\rightarrow$ $\frac{1}{4} \times 21 \times \frac{22}{7} = 33$
P $\rightarrow$ $33 + 33 + 21 = 87cm$
The figure below is made up of three semi-circle and a circles. X is the center of the large semi-circle and WZ is 36cm. Find the area of the shaded part. Express your answer in terms of $\pi$.
Sorry. Please check the correct answer below.
Area of fig $\rightarrow$ $\frac{1}{2} \times 18 \times 18 \times \pi = 162\pi$
$\frac{1}{2} \times 36 \times 18 = 324$
$(162\pi - 324) ÷ 2 = 81\pi - 162$
$(20.25\pi – 40.5) \times 2 = 40.5\pi -81$
$(81\pi - 162) – (40.5\pi - 81) = (81\pi – 162)cm^2$
You are Right
Area of fig $\rightarrow$ $\frac{1}{2} \times 18 \times 18 \times \pi = 162\pi$
$\frac{1}{2} \times 36 \times 18 = 324$
$(162\pi - 324) ÷ 2 = 81\pi - 162$
$(20.25\pi – 40.5) \times 2 = 40.5\pi -81$
$(81\pi - 162) – (40.5\pi - 81) = (81\pi – 162)cm^2$
The figure is made of 2 similar segments of a circle. Find the perimeter of the figure.
Sorry. Please check the correct answer below.
Perimeter of figure $\rightarrow$ $(\frac{120}{360}\times 2^\pi \times 9) + 9 + 9 + 10 = (6^\pi + 28)$
You are Right
Perimeter of figure $\rightarrow$ $(\frac{120}{360}\times 2^\pi \times 9) + 9 + 9 + 10 = (6^\pi + 28)$
Elvin had a circular piece of paper. She folded it into quarters and than cut away a semicircle, a quarter circle and a quarter circle and a square from the corners as shown below. Find the perimeter of the paper left after Elvina unfolded the paper. $(Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
$6 \times 6 = 36$
$3.14 \times 22 = 69.08$
$2 \times 3.14 \times 6 = 37.68$
$2 \times (\frac{1}{2} \times 3.14 \times 8 \times 8) = 41.12$
$6 \times 4 = 24$
$41.12 + 24 + 37.68 + 69.08 = 171.88cm$
You are Right
$6 \times 6 = 36$
$3.14 \times 22 = 69.08$
$2 \times 3.14 \times 6 = 37.68$
$2 \times (\frac{1}{2} \times 3.14 \times 8 \times 8) = 41.12$
$6 \times 4 = 24$
$41.12 + 24 + 37.68 + 69.08 = 171.88cm$
The figure below is made up of 2 semicircles with diameters 7cm and 14cm respectively. What is the perimeter of the figure? $(Take \pi = \frac{22}{7})$
Sorry. Please check the correct answer below.
$\frac{1}{2} \times \frac{22}{7} \times 14 = 22$
$\frac{1}{2} \times \frac{22}{7} \times 7 = 11$
$ 22 + 11 + 3.5 + 3.5 = 40$
You are Right
$\frac{1}{2} \times \frac{22}{7} \times 14 = 22$
$\frac{1}{2} \times \frac{22}{7} \times 7 = 11$
$ 22 + 11 + 3.5 + 3.5 = 40$
The figure below is made up of a quadrant and 2 identical semicircles of radius 10.5cm. Find the perimeter of the figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
$\frac{1}{4} (2 \times \frac{22}{7} \times 10.5) \times 1\frac{1}{4} = 82.5$
$82.5 + 10.5 + 10.5 = 103.5cm$
You are Right
$\frac{1}{4} (2 \times \frac{22}{7} \times 10.5) \times 1\frac{1}{4} = 82.5$
$82.5 + 10.5 + 10.5 = 103.5cm$
The figure below is made up of squares EFGH and PQRS, a circle and two identical semicircles. J and K are the midpoints of PQ and RQ respectively. P,Q, R and S are the midpoints of EF, FG, GH and EH respectively. Use the calculator value of $\pi$ to find the total area of the shaded parts, correct to 2 decimal places.
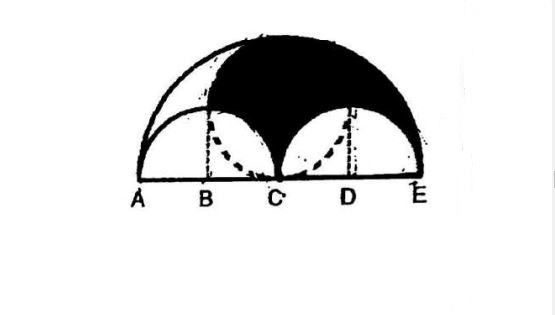
Sorry. Please check the correct answer below.
Area A = $(Area of quadrant – area of triangle)$ ÷ 4 = $(\pi \times 14 \times 14 \times \frac{1}{4} - \frac{1}{2} \times 14 \times 14) = 55.94cm^2$
Area of triangle = $\frac{1}{2} \times 14 \times 7 = 49cm^2$
Total area of shaded parts = $55.94 + 49 = 104.94cm^2$
You are Right
Area A = $(Area of quadrant – area of triangle)$ ÷ 4 = $(\pi \times 14 \times 14 \times \frac{1}{4} - \frac{1}{2} \times 14 \times 14) = 55.94cm^2$
Area of triangle = $\frac{1}{2} \times 14 \times 7 = 49cm^2$
Total area of shaded parts = $55.94 + 49 = 104.94cm^2$
The figure below is made up of a right- angled triangle and a circle overlapping two semicircles. AC is the diameter of the circle. $ (Take\pi = 3.14)$
(a) Find the perimeter of the shaded parts.
(b) Find the total area of the shaded parts.
(b) 20
(b) 22
(b) 24
(b) 26
Sorry. Please check the correct answer below.
(a) $\frac{1}{2} \times 3.14 \times 10 = 15.7$
$\frac{1}{2} \times 3.14 \times 6 = 9.42$
$\frac{1}{2} \times 3.14 \times 8 – 12.56$
$15.7 + 9.24 + 12.56 = 37.68$
(b) $\frac{1}{2} \times 6 \times 8 = 24$
$\frac{1}{2} \times 3.14 \times 3 \times 3 + \frac{1}{2} \times 3.14 \times 4 \times 4 = 39.25$
$\frac{1}{2} \times 3.14 \times 5 \times 5 = 39.25$
$39.25 + 24 – 39.29 = 24$
(b) 24
You are Right
(a) $\frac{1}{2} \times 3.14 \times 10 = 15.7$
$\frac{1}{2} \times 3.14 \times 6 = 9.42$
$\frac{1}{2} \times 3.14 \times 8 – 12.56$
$15.7 + 9.24 + 12.56 = 37.68$
(b) $\frac{1}{2} \times 6 \times 8 = 24$
$\frac{1}{2} \times 3.14 \times 3 \times 3 + \frac{1}{2} \times 3.14 \times 4 \times 4 = 39.25$
$\frac{1}{2} \times 3.14 \times 5 \times 5 = 39.25$
$39.25 + 24 – 39.29 = 24$
The figure below, not drawn to scale, shows a three- quarter circle. Find its perimeter $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
$\frac{3}{4} \times \frac{22}{7} \times 14 = 33$
$33 + 7 + 7 = 47cm$
You are Right
$\frac{3}{4} \times \frac{22}{7} \times 14 = 33$
$33 + 7 + 7 = 47cm$
A rectangle is placed in a circle with O as center. Use the calculator value of $\pi$ to find the shaded part of the circle
Sorry. Please check the correct answer below.
radius $\rightarrow$ 10cm; Shaded part $\rightarrow$ $\frac{3}{4} \times \pi \times 10cm \times 10cm = 235.62cm^2$
You are Right
radius $\rightarrow$ 10cm; Shaded part $\rightarrow$ $\frac{3}{4} \times \pi \times 10cm \times 10cm = 235.62cm^2$
The figure below is made up of 4 identical circle, each with a radius of 7cm. The circle overlap at the shaded parts A, B and C. The area of the shaded part is 30cm$^2$. . Find the total area of the unshaded parts. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The area of rectangle WXYZ is 98cm$^2$. Find the radius of the seim-circle. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The figure below is formed by 3 circles with the same center. Their radii is in the ratio 2 : 3 : 4. The diameter of the smallest circle is 4cm. Find the diameter of the smallest circle is 4cm. Find the area of the shaded parts.
Sorry. Please check the correct answer below.
You are Right
The figure below shown the design of a floor rug. The edges of the rug is made up of 4 semicircles and 4 quarter-circle, each of radius 21cm. $(Take\pi = \frac{22}{7})$ .
(a) Find the perimeter of the rug.
(b) Find the area of the rug.
(b) 6479cm$^2$
(b) 7594cm$^2$
(b) 8568cm$^2$
(b) 9625cm$^2$
Sorry. Please check the correct answer below.
(a) $132 \times 3 = 396$
(b) 8568cm$^2$ $\rightarrow$ Total area $\rightarrow$ $2772= 1386 + 882 + 3528 = 8568$
(b) 8568cm$^2$
You are Right
(a) $132 \times 3 = 396$
(b) 8568cm$^2$ $\rightarrow$ Total area $\rightarrow$ $2772= 1386 + 882 + 3528 = 8568$
The shaded figure below is formed by semicircles, quarter circle and squares. ABEF is a square. What is the area of the shaded region?
Sorry. Please check the correct answer below.
Area of rectangle: $30 \times 60 = 1800cm^2$
Area of semicircle: $\frac{1}{2} \times 30 \times 30 \times 3.14 = 141cm^2$
$1800cm^2 - 1413cm^2 = 387cm^2$
Area of circle: $15 \times 15 \times 3.14 = 706.5cm^2$
$706.5cm^2 + 387cm^2 = 1093.5cm^2$
You are Right
Area of rectangle: $30 \times 60 = 1800cm^2$
Area of semicircle: $\frac{1}{2} \times 30 \times 30 \times 3.14 = 141cm^2$
$1800cm^2 - 1413cm^2 = 387cm^2$
Area of circle: $15 \times 15 \times 3.14 = 706.5cm^2$
$706.5cm^2 + 387cm^2 = 1093.5cm^2$
The figure is made up of a rectangle and two quarter circle. The breadth of the rectangle is 10cm. what is the total area of the shaded parts?
Sorry. Please check the correct answer below.
You are Right
The figure shows 4 identical in a square, ABCD. The area of the square is 64cm$^2$. Find the area of the shaded part. $ (Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
$180 – 105 – 30 = 45$
$180 – 85 – 45 = 50$
$180 – 50 = 130$
$130 \div 2 = 65^\circ$
You are Right
$180 – 105 – 30 = 45$
$180 – 85 – 45 = 50$
$180 – 50 = 130$
$130 \div 2 = 65^\circ$
The figure below is made up of 2 identical quadrants and 2 identical semicircles. Find the area of the shaded part of the figure. $(Take \pi = \frac{22}{7})$.
Sorry. Please check the correct answer below.
You are Right
The figure below is made up of big circle, a small circle and a square. The comers of the square touch the circumference of the circle. The radius of the small circle is 8cm. The area of the square is 256cm $^2$. Find the area of the shaded part. $ (Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
$256 \times \frac{1}{4} = 64$
R \times r = 128
BQ$\rightarrow$ $\frac{1}{4} \times 3.14 \times 128 = 100.48$
SQ $\rightarrow$ $\frac{1}{4} \times 3.14 \times 8 \times 8 = 50.24$
$100.48 – 50.24 = 50.24cm^2$
You are Right
$256 \times \frac{1}{4} = 64$
R \times r = 128
BQ$\rightarrow$ $\frac{1}{4} \times 3.14 \times 128 = 100.48$
SQ $\rightarrow$ $\frac{1}{4} \times 3.14 \times 8 \times 8 = 50.24$
$100.48 – 50.24 = 50.24cm^2$
The figure below is made up of a semicircle, a square and 3 quadrants. The side of the square is 20cm. For each of the following, use the calculator value of $\pi$ to find
(a) The area of the shaded part, correct to 2 decimal places.
(b) The perimeter of the shaded part, correct to 2 decimal places.
(b) 166.50cm
(b) 177.50cm
(b) 188.50cm
(b) 199.50cm
Sorry. Please check the correct answer below.
(a) $\frac{3}{4} \times \pi \times 20\times 20 = 300\pi$
$\frac{1}{4} \times \pi \times 40\times 40 = 400\pi$
$20 \times 20 = 400$
$\frac{1}{4} \times \pi \times 20\times 20 = 100\pi$
$400\pi – 100\pi – 400 = 300\pi – 400$
$300\pi – 400 + 300\pi = 1481.96cm^2$
(b) $\pi \times 40 = 40\pi$
$\pi \times \frac{1}{4} \times 80 = 20\pi$
$20\pi + 40\pi = 188.50cm$
(b) 188.50cm
You are Right
(a) $\frac{3}{4} \times \pi \times 20\times 20 = 300\pi$
$\frac{1}{4} \times \pi \times 40\times 40 = 400\pi$
$20 \times 20 = 400$
$\frac{1}{4} \times \pi \times 20\times 20 = 100\pi$
$400\pi – 100\pi – 400 = 300\pi – 400$
$300\pi – 400 + 300\pi = 1481.96cm^2$
(b) $\pi \times 40 = 40\pi$
$\pi \times \frac{1}{4} \times 80 = 20\pi$
$20\pi + 40\pi = 188.50cm$
The figure below, not drawn to scale, shows a circle overlapping a larger semi circle. If the ratio of the shaded area to unshaded area is 5: 8, Find the ratio of the radius of the circle to the radius of the larger semi- circle.
Sorry. Please check the correct answer below.
Shahed:Unshaed
5:8
$5 + 4 = 9$
$\sqrt(9)=3
$Big Semicircle = 9Units
Small Semicirlce = 4Units
$\sqrt(4)=2$
Ratio = 2:3
You are Right
Shahed:Unshaed
5:8
$5 + 4 = 9$
$\sqrt(9)=3
$Big Semicircle = 9Units
Small Semicirlce = 4Units
$\sqrt(4)=2$
Ratio = 2:3
The figure below shows a triangle enclosed within a semicircle O is the center of the semicircle. Find the area of the shaded part. $ (Take\pi = 3.14)$.
Sorry. Please check the correct answer below.
Triangle = $\frac{1}{2} \times 16 \times 9.6 = 76.8$
$16 \div 2 = 8$
$3.14 \times 8 \times 8 \frac{1}{2} = 100.48$
$100.48 – 76.8 = 23.68cm^2$
You are Right
Triangle = $\frac{1}{2} \times 16 \times 9.6 = 76.8$
$16 \div 2 = 8$
$3.14 \times 8 \times 8 \frac{1}{2} = 100.48$
$100.48 – 76.8 = 23.68cm^2$
PSLE-Math.com
Start winning at math! Be part of Singapore PSLE Math community and Unleash the Your Maths Potential!
General
2026 © All Rights Reserved. Privacy Policy | Terms of Service
What subject area do you need help in?
Select level
Select subject
